運動方程

　　在傳遞過程的研究中，指流動流體的微分動量衡算式，是描述粘性流體流動的基本方程之一。此方程與連續性方程和各種具體問題的定解條件相結合，可求解速度分佈和壓力分佈。

　　運動方程建立在牛頓第二定律基礎上，表示流體動量的變化率（即流體品質與其加速度的乘積）等於作用於流體上外力的合力。所考慮的外力有兩類：作用在整個流體品質上的力，即體積力（如重力）；和作用在邊界上的力，即表面力（如壓力和剪切力）。運動方程的向量式為：

　　　　　　　　　(1)

式中 F為單位體積力，如單位體積重力， F＝ ρg， ρ為流體密度， g為重力加速度； p為單位體積邊界上的力； u為速度； τ為時間； D u/ D τ為加速度。 D u/ D τ稱為隨體導數，並記作D/ D τ，以區別於常用的d/ d τ。

　　法國科學傢C.-L.-M.-H.納維在1827年和G.G.斯托克斯在1845年分別將式(1)與廣義牛頓定律結合，得到描述牛頓粘性流體流動時的微分方程式，即納維－斯托克斯方程，它在直角坐標系中可寫成：

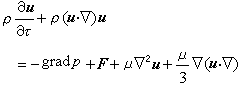
　　(2)

對於不可壓縮流體， u·▽＝0，式(2)變為：

　　　(3)

式(3)是應用最廣的運動方程。與式(1)對比可知方程左側是流體的慣性力向量，其中加速度 D u/ D τ分成瞭兩項：①д u/д τ為局部加速度，指流體速度 u隨時間 τ的變化率；②( u·▽) u為對流加速度，指流體因位置變化所引起的加速度。方程右側 F（體積力）形式未變， p（表面力）則表示為壓力梯度（右側第一項）及粘性力向量（右側第三項）。

　　在直角坐標系中，式(3)的x方向分量式為：

　　(4)

　　理想流體運動方程　忽略流體的粘性，即對於理想流體，納維－斯托克斯方程中右側第三、四兩項為零，這就是由瑞士數學傢和力學傢L.歐拉於1755年提出的歐拉方程：

歐拉方程於定態條件下沿流線（流動空間中某瞬時的這樣一種曲線，其上各質點的流速方向與該點的切線重合）積分，即是 伯努利方程。

　　湍流運動方程　對於湍流運動，將不規則變化的瞬時速度u和瞬時壓力p分別分解為時均速度ū 和脈動速度u′，以及時均壓力p和脈動壓力p′，則有u＝ū＋u′，p＝p+p′，將此兩式代入式(4)，可得到湍流運動方程，寫成分量形式，以x方向為例：

　　　(5)

對於 y、 z方向亦有類似形式，這組方程稱為雷諾方程。

　　將雷諾方程與納維-斯托克斯方程對比，可以看出前者多瞭幾個附加項，這是由於湍流脈動所引起各個方向的應力，即

等，稱為湍流應力或雷諾應力。

　　對於兩相流和非牛頓流體流動，運動方程的建立和求解有很多困難，至今還很不成熟，但鑒於這些流動在工程上的重要性，是目前研究工作十分活躍的領域。

　　應用　納維－斯托克斯方程和連續性方程一起，構成牛頓粘性流體運動的基本方程組。由於方程是非線性的，至今尚無一般解，隻能結合特定情況處理。對於一些簡單的問題，非線性項為零或是非常簡單的形式，可得精確解。對於較復雜的情況，有時根據流動問題的物理特點，可以略去方程中的次要項，簡化成近似方程後求解。如在低雷諾數時，忽略慣性力，所得近似方程稱為爬流方程。由後者求解得到著名的斯托克斯定律（見流動阻力）；在高雷諾數時，用邊界層概念簡化運動方程，可瞭解繞流和射流的特征。此外，用數值法解這組方程，可以解決更復雜的問題，例如攪拌槽中粘稠液體的運動、波動液膜的運動以及伴有化學反應的湍流運動等。